Question

Write the equation in slope intercept form.We have two points that belong to the line: (1,3) and (4,9)

Answer 1

We have two points of the line, and we have to find the equation of the line in the slope-intercept form:

`y=mx+b`

First, we find the slope as:

`m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(9-3)/(4-1)=(6)/(3)=2`

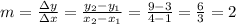
With the value of the slope, we can calculate b replacing the values of x and y with one of the know points:

`\begin{gathered} y=mx+b \\ y=2x+b \\ 3=2\cdot1+b \\ 3=2+b \\ b=3-2 \\ b=1 \end{gathered}`

Now, we have the two parameters (slope and y-intercept) to define the line, and we can write the equation as:

`y=2x+1`