To draw any line on the plane, locate two points on it and cross them using a straight line.
Then, in our case, we need to find two points on each of the two lines
As for y= -x-3
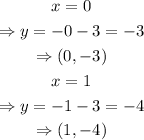
Similarly, in the case of x-3y=-3
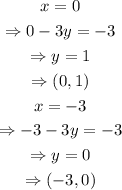
Using the first set of points, graph y= -x-3, as shown below
Graphing the second line, x-3y=-3
Graph both lines at the same time and look for the intersection point
Then, the solution to the system of equations is (x,y)=(-3,0)