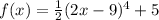Answer:
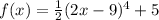
Explanation:
Given f'(x) defined below:
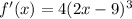
First, integrate f'(x) to find f(x).
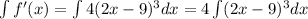
Let u = 2x-9
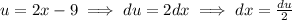
Thus:
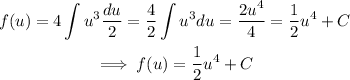
Replace u=2x-9.
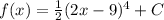
Next, using the point (5,11/2), we find the value of C, the constant of integration.
At (5, 11/2)
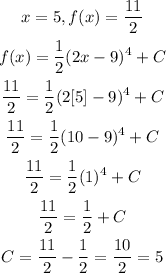
Therefore, the function f(x) is: