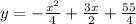Question

Write the equation of each parabola based on the given information. Focus = 3,6Directrix y=8

Answer 1

To write the equation of a parabola, we are given the following information;

`\begin{gathered} \text{Focus}=(3,6) \\ \text{Directrix;} \\ y=8 \end{gathered}`

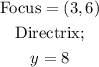
We shall begin by taking any point on the parabola which would be point;

`(x_1,y_1)`

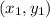
The distance between the focus and this random point can be calculated as follows;

`d=\sqrt[]{(x_1-3)^2+(y_1-6)^2}`

Similarly, the distance between the directrix and this random point is;

`|y_1-8|`

Note that the directrix is given as

`\begin{gathered} y=8 \\ \text{Therefore;} \\ The\text{ two y-coordinates would be;} \\ y_1\text{ and} \\ y=8 \\ \text{The distance therefore is, } \\ y_1-8 \end{gathered}`

This is expressed in absolute value because the distance cannot be a negative.

We now equate both distances and we can begin to simplify;

`\begin{gathered} \sqrt[]{(x_1-3)^2+(y_1-6)^2}=|y_1-8| \\ \text{Square both sides of the equation to eliminate the radical;} \\ (x_1-3)^2+(y_1-6)^2=(y_1-8)^2 \\ \end{gathered}`

We can now simplify all parenthesis;

`x^2_1-6x_1+9+y^2_1-12y_1+36=y^2_1-16y_1+64`

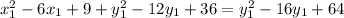
We now move all terms to one side and we now have;

`\begin{gathered} x^2_1-6x_1+9-64+y^2_1-y^2_1-12y_1+16y_1=0 \\ x^2_1-6x_1-55+4y_1=0 \end{gathered}`

Next step, we make y the subject of the formula;

`\begin{gathered} 4y_1=-x^2_1+6x_1+55 \\ \text{Divide all through by 4;} \\ y_1=-(1)/(4)x^2_1+(3)/(2)x_1+(55)/(4) \end{gathered}`

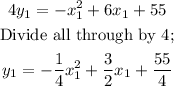
We can now re-write for (x, y) as follows;

ANSWER:

`y=-(x^2)/(4)+(3x)/(2)+(55)/(4)`