In order to determine the system of equation for this graph, we need to first identify two points on each slanting line and just one point for the horizontal line.
Now that we have identified two points on each slanting line, let's use the Two-Point Form formula to determine the equation.
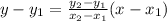
Let's start with the solid line. Let's plug in the two red points in the graph and simplify.
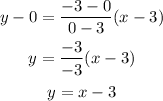
Hence, the equation of the solid line is y = x - 3. However, since the shade of the line is below the line, the equation is y ≤ x - 3.
Let's move on to the broken line. Let's plug in the coordinates of the two green points into the formula. Then, solve for y.
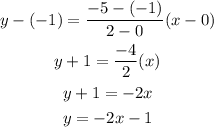
The equation of the broken line is y = -2x - 1. However, since the shade is above the dashed line, the equation is y > -2x - 1.
Lastly, for the third dashed line, the horizontal straight dashed line, the equation is y = -6 however, since the shade is above the dashed line, the equation will be y > -6.
To summarize, the system of equations are:
solid line: y ≤ x - 3
slanting dashed line: y > -2x - 1.
horizontal dashed line: y > -6