Question

A company producing jigsaw puzzles has fixed costs of $6250 and variable costs of $13 per puzzle. The company sells thepuzzles for $15 each.(C) Find the profit function in terms of q.Profit(q)(D) Find the Break-Even point in ordered pair form.Break-Even Point =(E) How many puzzles must be produced and sold so you will realize a profit of $19600? You may want to solve algebraicallyor graphically.q=

Answer 1

• C. P(q)=2q-6250

,

• D. The break-even point is (q, P(q))=(3125, 0).

,

• E. 12,925 puzzles

Explanation:

• Fixed Cost = $6250

,

• Variable Cost = $13 per puzzle

The total cost for producing q puzzles is:

`C(q)=6250+13q`

The company sells the puzzles for $15 each. Thus, the revenue from selling q puzzles is:

`R(q)=15q`

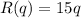
Part C

`\begin{gathered} Profit=Revenue-Cost \\ P(q)=R(q)-C(q) \\ =15q-(6250+13q) \\ P(q)=2q-6250 \end{gathered}`

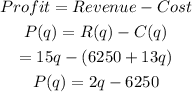
The profit function is P(q)=2q-6250.

Part D

The break-even point is the point at which the profit is $0, i.e. when revenue is equal to the cost.

`\begin{gathered} P(q)=0 \\ 2q-6250=0 \\ 2q=6250 \\ q=(6250)/(2) \\ q=3125 \end{gathered}`

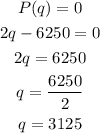
The break-even point is (q, P(q))=(3125, 0).

Part E

When the profit, P(q)=$19600

`\begin{gathered} P(q)=19600 \\ 2q-6250=19600 \\ 2q=6250+19600=25850 \\ q=(25850)/(2) \\ q=12,925 \end{gathered}`

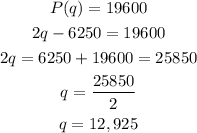
To realize a profit of $19,600, 12,925 puzzles must be produced and sold.