Question

Which equation is perpendicular to y= -5/3x - 6y= -5/3x - 3y= 5/3x + 7y= -3/5x + 4y= 3/5x - 10

Answer 1

Two lines are perpendicular if and only if their slopes fulfil:

`m_1m_2=-1`

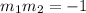
All of the equations are given in the form:

`y=mx+b`

Then, the equation

`y=-(5)/(3)x-6`

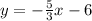
has slope:

`m_1=-(5)/(3)`

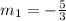
Plugging this in the perpendicular relation we have that:

`\begin{gathered} -(5)/(3)m_2=-1 \\ m_2=(-1)/(-(5)/(3)) \\ m_2=(3)/(5) \end{gathered}`

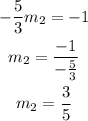
this means that any perpendicular line to the one given has to have slope 3/5.

From the options given we notice that the only line that has this slope is:

`y=(3)/(5)x-10`

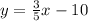
Therefore, the perpendicular line is the last option.