Diagram:
From the above right triangle, we can stablish the following:
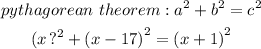
Solving for x:
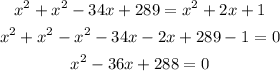
apply the quadratic formula,
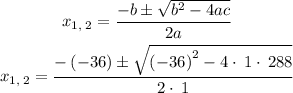
then,
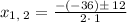
separate the solutions,
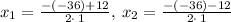
Thus,

since, the shadow is x-17 meters long, then any value below 17 does not make much sense, therefore,
The answer is, x = 24