Question

rectFind the equation in slope-intercept form) of the line with the given slope that passes through the pointwith the given coordinates.slope:2- 32ordered pair: (-3,-2)AncilorKeypad

Answer 1

`y=-(3)/(2)x-(13)/(2)`

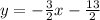
Explanations:

The equation of a line in point-slope form is expressed as:

`y-y_0=m(x_{}-x_0)`

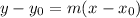
where:

• m is the, slope ,of the line

,

• (x0, y0) is, any point ,on the line

Given the following parameters

`\begin{gathered} m=-(3)/(2) \\ (x_0,y_0)=(-3,-2) \end{gathered}`

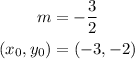
Substitute the given parameters into the formula to have:

`\begin{gathered} y-(-2)=-(3)/(2)(x_{}-(-3)) \\ y+2=-(3)/(2)(x+3) \\ 2(y+2)=-3(x_{}+3) \end{gathered}`

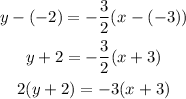
Expand and write in slope-intercept form y = mx + b

`\begin{gathered} 2y+4=-3x-9 \\ 2y=-3x-9-4 \\ 2y=-3x-13 \\ y=-(3)/(2)x-(13)/(2) \end{gathered}`

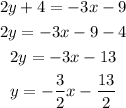
Hence the equation of the line in slope-intercept form is expressed as

y = -3/2x - 13/2