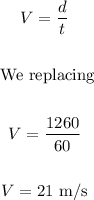ANSWER:
a)
b) 28 m/s
c) 60 sec
d) -2.8 m/s^2
e) 21 m/s
Explanation:
For t = 0 s to t = 20 s
a = 1.4 m/s ^2
u = 0 m/s
Therefore:
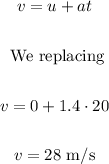
(a)
Knowing this, we can sketch the velocity-time graph:
(b)
The maximum speed can be determined in the graph and is 28 m/s
(c)
Area under v-t graph gives displacement:
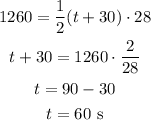
So the total time is 60 seconds
(d)
Using between t = 50 and t = 60
t = 60 - 50 = 10 sec
u = 28 m/s
v = 0
We solving for a:
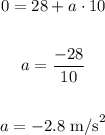
(e)
The average speed is the distance traveled in the total time, therefore: