Question

Past experience shows that Mr. Reisman will have 3 left-handed students in every class of 25 math students.If Mr. Reisman teaches 125 students in one day, what is the most likely total number of left-handed students in his classes?O A. 12O B. 3O c. 15OD. 125O E: 22

Answer 1

Mr Reisman have some data available of his class frm past. This data described the number of left handed students in a math class.

We will first define/assign variables to each of the numbers i.e ( number of left handed students ) and ( number of students in the class ).

`\begin{gathered} x\text{ = number of left handed students} \\ y\text{ = number of students in math class} \end{gathered}`

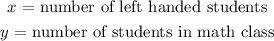
Now we will go ahead and define the relationship between these two variables ( x and y ) defined above.

We see that if i increase the size of math class i.e ( value of variable y ) then the likelyhood of left-handed students increases i.e ( value of x increaes ). We can associate such relationships with propotions. To classify this type we can categorize as " direct proportions ".

We will go ahead and express our proportionality ( direct ) relation of two vairbales ( x and y ) in a mathematical form as follows:

`y\text{ = k}\cdot x`

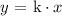
Where,

`\text{ k = constant of proportionality}`

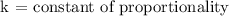
The general equation that can be used for forecasting or evaluating values for different class size and number of left handed students can be expressed in the form as follows:

`(y_0)/(x_0)\text{ = }(y_1)/(x_1)`

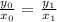
The above equation is a basic manipulation of equating the limit of proportionality for two class different math class sizes where,

`\begin{gathered} y_{o\text{ }}=25,orignal\text{ math class size ( as per past data )} \\ x_o\text{ = 3, original number of left handed students ( as per data )} \\ y_{1\text{ }}=\text{ 125 , the new class size} \\ x_1\text{ = The expected number of left handed students in the new class} \end{gathered}`

So, we are have three known quantities and one unknown ( x1 ). We can plug in the above quantities in the generalized equation above and solve for ( x1 ) as follows: