Question

QuestionUse trigonometric identities, algebraic methods, and inverse trigonometric functions, as necessary, to solve the following trigonometric equation on the interval [0, 22).Round your answer to four decimal places, if necessary. If there is no solution, indicate "No Solution."12sin?(x) - 20sin(x) = -8

Answer 1

`x=(1)/(2)\pi rads,\text{ 0.2323}\pi rads`

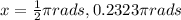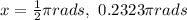
STEP - BY - STEP EXPLANATION

What to do?

Solve the given trigonometric equation.

Given:

`12\sin ^2x-20\sin x=-8`

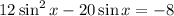
To solve the given problem, we will follow the steps below:

Step 1

Let y=sinx

Step 2

Replace sinx by y.

`12y^2-20y=-8`

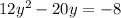
Step 2

Re-arrange the above into the form:

`ax^2+bx+c=0_{}`

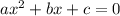
That is;

`12y^2-20y+8=0`

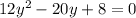
a=12 b=-20 and c=8

Step 3

Use the quadratic formula below to solve.

`y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`
`y=\frac{20\pm\sqrt[]{(-20)^2-4(12)(8)}}{2(12)}`
`=\frac{20\pm\sqrt[]{400-384}}{24}`
`\begin{gathered} =\frac{20\pm\sqrt[]{16}}{24} \\ \\ =(20\pm4)/(24) \end{gathered}`

Either

`\begin{gathered} y=(20+4)/(24)=(24)/(24)=1 \\ \\ or \\ \\ y=(20-4)/(20)=(16)/(24)=(2)/(3) \end{gathered}`

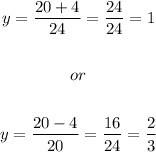
Step 4

Substitute the value of y in;

y=sinx

If y = 1

Then,

`\sin x=1`
`x=\sin ^(-1)(1)`
`x=90\degree`
`\begin{gathered} x=90*(\pi)/(180) \\ \\ =(\pi)/(2)\text{rads} \end{gathered}`

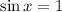
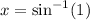
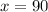
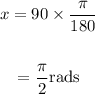
Step 5

Substitute y=2/3 in y=sinx

`\sin x=(2)/(3)`
`x=\sin ^(-1)((2)/(3))`
`x=41.8103148958\degree`

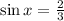
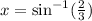
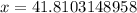
Change to radians

`x=41.8810348958*(\pi)/(180)`
`=0.2323\pi rads`

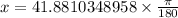
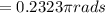
Therefore,

`x=(1)/(2)\pi rads,0.2323\pi rads`