Given:
Angle B = 103 degrees
Angle C = 28 degrees
Side b = 52 units
Find: measures of Angle A, side a, and side c.
Solution:
First, let's solve for the measure of Angle A.
Recall that the sum of the interior angles of a triangle is 180°. This means:
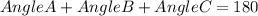
Since we already know the measure of angles B and C, we can subtract it from the total measure which is 180° to solve for the measure of Angle A.
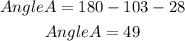
Therefore, the measure of Angle A is 49°.
Next, let's solve for the measure of side c using Sine Law.
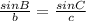
Let's plug into the equation above the value of B, C, and b.
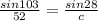
Then, solve for the value of c.
Cross multiply.
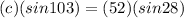
Divide both sides by sin 103.
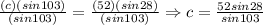
Evaluate the value of "c" using a calculator.
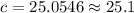
The measure of side c is approximately 25.1 units.
Lastly, to solve for the measure of side "a", we will still use sine Law.
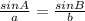
Let's plug into the equation above the value of A, B, and b.
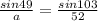
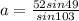
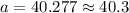
The measure of side a is approximately 40.3 units.