Given:
Interest rate = 2.5% compounded quarterly
Final Amount = $20,000
Time = 15 years
Let's find the amount you should invest in the account.
Here, we are to find the principal amount.
Apply the formula:

Where:
A is the final amount = $20,000
r is the rate = 2.5% = 0.025
compound frequency is n. Since it is compounded quarterly, n = 4
t is the time in years = 15 years.
Let's solve for P.
We have:
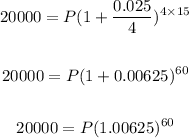
Solving further:
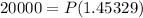
Divide both sides by 1.45329:

Therefore, the amount that should be invested is $13,761.87
ANSWER:
$13,761.87