Question

I am not sure. but i got as far as, is this close? i am not sure.

Answer 1

5√6 mi

Step-by-step explanation:

In the given figure, triangles DAC and EBC are similar.

The ratio of corresponding sides are:

`(DA)/(EB)=(AC)/(BC)=(DC)/(EC)`

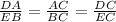
Substitute the given values:

`\begin{gathered} \frac{4\sqrt[]{138}}{\sqrt[]{138}}=\frac{BC+6\sqrt[]{3}}{BC} \\ 4=\frac{BC+6\sqrt[]{3}}{BC} \\ 4BC=BC+6\sqrt[]{3} \\ 4BC-BC=6\sqrt[]{3} \\ 3BC=6\sqrt[]{3} \\ BC=\frac{6\sqrt[]{3}}{3} \\ BC=2\sqrt[]{3} \end{gathered}`

Since we already have BC and EB, we use the Pythagoras theorem:

`\begin{gathered} EC^2=EB^2+BC^2 \\ EC^2=(\sqrt[]{138})^2+(2\sqrt[]{3})^2 \\ EC^2=138+12 \\ EC^2=150 \\ EC^{}=√(150) \\ EC=5√(6)\text{ mi} \end{gathered}`

The exact length of EC is 5√6 mi.