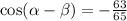Question

I need help with this practice Having trouble with itIt’s from the trigonometry portion of my ACT prep guide *in the box is my attempted answer for this, so disregard until you complete this

Answer 1

We know that:

`\cos (\alpha-\beta)=\sin (\alpha)\sin (\beta)+\cos (\alpha)\cos (\beta)`

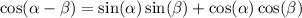
Let's take a closer look at alpha. We know that:

`\begin{gathered} \tan ^2(\alpha)=\sec ^2(\alpha)-1 \\ \rightarrow\tan ^2(\alpha)=(1)/(\cos^2(\alpha))-1 \\ \\ \rightarrow\tan ^2(\alpha)+1=(1)/(\cos^2(\alpha)) \\ \\ \rightarrow\cos ^2(\alpha)=(1)/(\tan^2(\alpha)+1) \\ \\ \rightarrow\cos ^{}(\alpha)=\pm\text{ }\sqrt[]{(1)/(\tan^2(\alpha)+1)} \end{gathered}`

We also know that alpha is in quadrant II, where cosine is negative. This way,

`\begin{gathered} \cos ^{}(\alpha)=-\text{ }\sqrt[]{(1)/(\tan^2(\alpha)+1)} \\ \\ \rightarrow\cos ^{}(\alpha)=-\text{ }\sqrt[]{(1)/((-(12)/(5))^2+1)} \\ \\ \Rightarrow\cos (\alpha)=-(5)/(13) \end{gathered}`

We also know that:

`\tan (\alpha)=(\sin(\alpha))/(\cos(\alpha))\rightarrow\sin (\alpha)=\tan (\alpha)\cos (\alpha)`

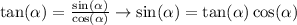
This way,

`\begin{gathered} \sin (\alpha)=(-(12)/(5))(-(5)/(13)) \\ \\ \Rightarrow\sin (\alpha)=(12)/(13) \end{gathered}`

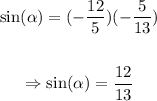
We can conclude that:

`\begin{gathered} \sin (\alpha)=(12)/(13) \\ \cos (\alpha)=-(5)/(13) \end{gathered}`

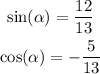
Now, let's take a closer look at beta. We know that:

`\begin{gathered} \sin ^2(\beta)=1-\cos ^2(\beta) \\ \rightarrow\sin (\beta)=\pm\text{ }\sqrt[]{1-\cos^2(\beta)} \end{gathered}`

And since beta lies in quadrant 4, where sine is negative,

`\begin{gathered} \sin (\beta)=-\text{ }\sqrt[]{1-\cos^2(\beta)}\rightarrow\sin (\beta)=-\text{ }\sqrt[]{1-((3)/(5))^2} \\ \\ \Rightarrow\sin (\beta)=-(4)/(5)_{} \end{gathered}`

This way, we can conclude that

`\begin{gathered} \sin (\beta)=-(4)/(5) \\ \cos (\beta)=(3)/(5) \end{gathered}`

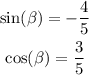
Now, we'll use the identity from the begining:

`\cos (\alpha-\beta)=\sin (\alpha)\sin (\beta)+\cos (\alpha)\cos (\beta)`

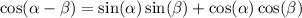
With the values we've calculated:

`\begin{gathered} \sin (\alpha)=(12)/(13) \\ \cos (\alpha)=-(5)/(13) \\ \text{and} \\ \sin (\beta)=-(4)/(5) \\ \cos (\beta)=(3)/(5) \end{gathered}`

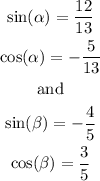
This way,

`\begin{gathered} \cos (\alpha-\beta)=\sin (\alpha)\sin (\beta)+\cos (\alpha)\cos (\beta) \\ \\ \rightarrow\cos (\alpha-\beta)=((12)/(13))(-(4)/(5))+(-(5)/(13))((3)/(5)) \\ \\ \Rightarrow\cos (\alpha-\beta)=-(63)/(65) \end{gathered}`

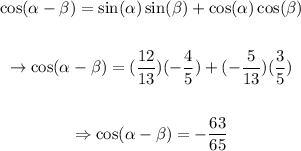
Therefore, we can conclude that:

`\cos (\alpha-\beta)=-(63)/(65)`