Question

The side of the second leg would be proximately blank inches long? Some help would be Greatly appreciate it thank you

Answer 1

Given: The dimension of the right-trinagle as

`\begin{gathered} H_{\text{ypothenuse}}=24\text{inches} \\ O_{ne\text{ of the legs of the triangle}}=12inches \end{gathered}`

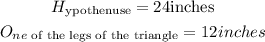
To Determine: The second leg of the triangle to the nearest tenth

Solution:

Let us represent the given using a right-triangle

The hypothenuse is the logest side and the side facing the right angle

Applying pythagoras theorem which state that the square of the hypothenuse is equal to the sum of the squares of the other sides

Let the other leg be y

Therefore

`y^2+12^2=24^2`
`\begin{gathered} y^2+144=576 \\ y^2=576-144 \\ y^2=432 \end{gathered}`
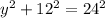
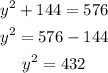
`\begin{gathered} y^2=432 \\ y=\sqrt[]{432} \\ y=20.7846 \\ y\approx20.8inches \end{gathered}`

Hence, the second leg of the triangle is 20.8 inches rounded to the nearest tenth