Question

Given the graph of f(x) above, find the value of integral(from 0 to 7) f(x)dx

Answer 1

The area under a curve between two points can be found out by doing the integral between the two points. In other words, the integral

Let's make a picture of the problem

Then, the integral will be equal to

`\int ^7_0f(x)dx\text{ = Area black zone + Area red zone + Area gr}een\text{ zone - Area blue zone}`

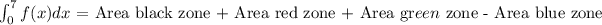
The area of the black region is given by the area of the triangular part plus the rectangular part, that is

`\begin{gathered} \text{ Area black zone = }(1)/(2)2*1+2*1 \\ \text{ Area black zone =}1+2 \\ \text{ Area black zone =}3 \end{gathered}`

The area of the red zone is the area of the rectangle

`\begin{gathered} \text{ Area red zone = 2}*2 \\ \text{ Area red zone =}4 \end{gathered}`

The green area is equal to the area of the green triangle,

`\begin{gathered} \text{ Area gre}en\text{ zone=}(1)/(2)1*2 \\ \text{ Area gre}en\text{ zone=}1 \end{gathered}`

and the blue area is the area of the blue triangle,

`\begin{gathered} \text{ Area blue zone = }(1)/(2)2*2 \\ \text{ Area blue zone = }2 \end{gathered}`

By substituting these values, the integral is given by

`\int ^7_0f(x)dx\text{ = }3+4+1-2`

Therefore, the answer is:

`\int ^7_0f(x)dx\text{ = }6`