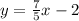Solution
- The question would like us to write the equation of the line passing through the points (0, -2) and (5,5) in slope-intercept form.
- The slope-intercept form of a linear equation is given by:

- The formula for solving this question is given below:
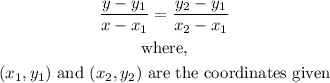
- The coordinates given are (0, -2) and (5,5)
- Thus, we can solve the question as follows

Final Answer