Answer:
irrational numbers and real numbers
Step-by-step explanation:
Given:

To find:
the number set the number belongs to
Rational numbers are numbers that can be written in fractional form. The roots of the perfect squares are rational numbers as they give whole numbers.
Irrational numbers are numbers that cannot be written in fractional form. The roots of non-perfect squares are irrational
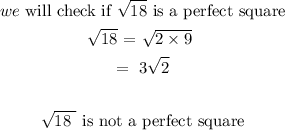
Hence, it is an irrational number
Whole numbers are whole with no decimals. Irrational numbers give decimals that do not end
Natural numbers are not irrational as the numbers are whole
Real numbers include both irrational numbers and rational numbers. As a result, √18 is a real number
Integers are natural numbers, opposites, and zero. They do not include decimals. Hence, they are rational
The correct answers are irrational numbers and real numbers