Question

Which shows the graph of the piecewise function given?Α) ΑB) BC CD D

Answer 1

Step-by-step explanation

A piecewise function is a function that is defined by different formulas or functions for each given interval.

So for the piecewise function given

`f(x)=\begin{cases}{(1)/(2)x+4,\text{ x}\leq-2} \\ {} \\ {-x,\text{ x>-2}}\end{cases}`

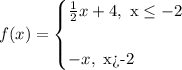
To plot the graph of the functions on the same axis

for the first function

`\begin{gathered} f(x)=(1)/(2)x+4 \\ we\text{ can find the value of f\lparen x\rparen, when x = -2,-3,-4} \\ when\text{ x=-2, f\lparen x\rparen=3} \\ when\text{ x=-3, f\lparen x\rparen=2.5} \\ when\text{ x=-4, f\lparen x\rparen=2} \end{gathered}`

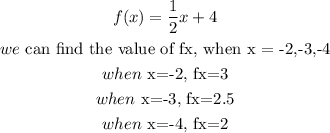
For the second function

`\begin{gathered} we\text{ can use when x = -1, y=-1} \\ when\text{ x=0, y=0} \\ \end{gathered}`

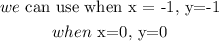
We can plot the x and f(x) coordiantes as:

in selecting the correct answer, we will have graph A as the correct graph

The answer is option A