Question

Twenty-eight people enter a tennis tournament. How many different first-round matches are possible if each player can be matched with any other player? matches

Answer 1

The given problem is a COMBINATION problem because Player A and Player B paired with each other is just similar to Player B and Player A.

The formula for combination is:

`\text{nCr}=(n!)/(r!(n-r)!)`

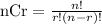
Our n = 28 and r = 2. Let's apply this to the formula above.

`\text{nCr}=(28!)/(2!(28-2)!)=(28!)/(2!26!)=(28*27)/(2)=(756)/(2)=378`

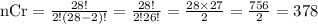
There are 378 possible different first-round matches.