Question

The problem is the first one illustrated. There is 2 answers that I have received through different sources, I am wondering which one is the correct answer. They are illustrated underneath the problem. Please just let me know which one is correct.

Answer 1

`\begin{gathered} \text{The rational function which gives the given condition} \\ f(x)\text{ = }\frac{2(x-2)^2\text{(x + 1)}}{3(x\text{ + 2)(x - 3)(x + 1)}} \end{gathered}`

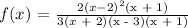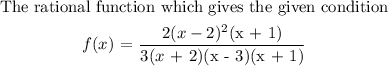
Step-by-step explanation:

comparing the two function you have:

2nd function:

`\begin{gathered} 2)\text{ }f(x)\text{ = }\frac{2(x-2)^2\text{(x + 1)}}{3(x\text{ + 2)(x - 3)(x + 1)}} \\ \\ In\text{ this function:} \\ x\text{ intercept: (x - 2) twice} \\ x\text{ - 2= 0} \\ x\text{ intercept: x = 2} \\ \\ The\text{ hole is factor co}mmon\text{ to both numerator and denominator} \\ (x\text{ + 1) is co}mmon\text{ to both numerator and denominator} \\ x\text{ + 1 = 0} \\ x\text{ = -1 (is a hole)} \\ \\ \text{vertical asymptote: Equate denominator to zero} \end{gathered}`

The difference between both functions is the x-intercept

The first function have two intercepts while the second function have only one x-intercept

From our question, the x intercept is supposed to be just 1

we were given the x-intercept as x = 2

Function has x -intercept as 2.

Function 2 is the correct representation of the rational function that gives those conditions in the question

`f(x)\text{ = }\frac{2(x-2)^2\text{(x + 1)}}{3(x\text{ + 2)(x - 3)(x + 1)}}`