Question

Question 24 In the accompanying diagram of right triangle ABC, a Fight angle is at C, AB = 26, and mZA = 27. Find the length of BC to the nearest tenth. B 26 27° A

Answer 1

hello

to solve this question, we should simply use trigonometric ratios SOHCAHTOA to determine which of the ratios to use

`\begin{gathered} \text{soh}=\sin \theta=(opp)/(hyp) \\ cah=\cos \theta=(adjacent)/(hypothenus) \\ \text{toa}=\tan \theta=(opposite)/(adjacent) \end{gathered}`

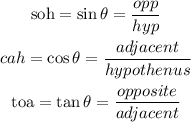
the diagram above is a representation of what we should reference to in terms of position of the sides in a triangle.

to find the length of BC, we have to use sine angle because we have the value of theta and hypothenus and we are solving for opposite

`\begin{gathered} \sin \theta=(opposite)/(hypothenus) \\ \theta=27 \\ hyp=26 \\ \sin 27=(BC)/(26) \\ BC=26*\sin 27 \\ BC=11.80 \end{gathered}`

from the calculation above, the length of line BC is equal to 11.80 units