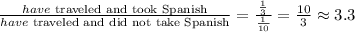Answer
It is 3.3 times as likely.
Explanation
From the graph, the fraction of students who traveled to a Spanish speaking country and took Spanish is:
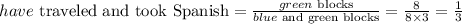
From the graph, the fraction of students who traveled to a Spanish speaking country and did not take Spanish is:
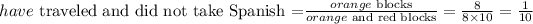
Then, the ratio between students who took Spanish and have traveled to a Spanish speaking country and students who did not take Spanish and have traveled to a Spanish speaking country is: