Question

Enter the coordinates of the vertex of the function f(x) = x2 + 4x - 7

Answer 1

Given the equation of the function:

`f(x)=x^2+4x-7`

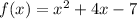
The given function represents a parabola

We will make a complete square to find the coordinates of the vertex

The coefficient of x = 4

Half the coefficient of x = 2

Square it give = 4

So, we will add and subtract 4

`\begin{gathered} f(x)=x^2+4x+4-4-7 \\ f(x)=(x^2+4x+4)-11 \\ f(x)=(x+2)^2-11 \end{gathered}`

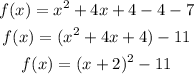
Compare the last equation with the vertex form of the parabola

`f(x)=(x-h)^2+k`

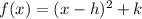
So, h = -2, k = -11

So, the answer will be the coordinates of the vertex = (-2, -11)