Answer:
a) The value of
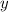 is 6.
is 6.
b) This line does not pass through the point of origin.
c)
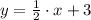 intersects with
intersects with
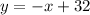 .
.
d) Both
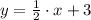 and
and
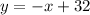 intersect in the first quadrant.
intersect in the first quadrant.
Explanation:
a) By Analytical Geometry, we know that an equation of the line can be found by knowing the coordinates of two distinct points on the plane. The equation of the line is defined by this formula:
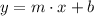 (1)
(1)
Where:
 - Independient variable.
- Independient variable.
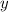 - Dependent variable.
- Dependent variable.
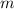 - Slope.
- Slope.
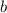 - x-Intercept.
- x-Intercept.
To determine the slope and x-intercept of the equation of the line, we have to solve the following system of linear equations:
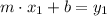 (2)
(2)
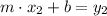 (3)
(3)
If we know that
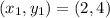 and
and
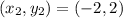 , then the solution of the system is:
, then the solution of the system is:
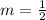 ,
,
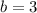
Then, the equation of the line is
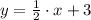 . If we know that
. If we know that
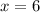 , then the value of
, then the value of
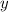 is:
is:
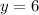
The value of
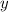 is 6.
is 6.
b) If this line passes through the point of origin, then the value of
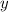 must be zero for
must be zero for
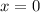 . If we know that
. If we know that
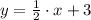 and
and
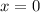 , then the value of
, then the value of
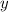 is:
is:
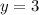
The line does not pass through the point of origin since x-intercept is not zero.
c) A system of two linear equations always has an unique solution if and only if slopes and x-intercepts are different to each other. This condition is satisfied by
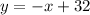 , so we conclude that both lines intersect each other.
, so we conclude that both lines intersect each other.
d) (Note: Question was incorrectly written. Correct form is: If your answer was yes in c, in which quadrant did they intersect?)
First, we solve the following system of linear equations:
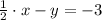 (4)
(4)
 (5)
(5)
The solution of this system is
 , which means that both lines intersects each other in the first quadrant.
, which means that both lines intersects each other in the first quadrant.