Question

With the wind, a plan flies 240 miles in 2 hours. Against the wind, the requires 3 hours to fly in the same distance. What is the rate of the wind?

Answer 1

Let x be the speed of the plane at not wind

Let y be the speed of the wind

Flying with the wind the effective speed is:

`x+y`

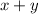
Flying against the wind the effective speed is:

`x-y`

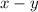
Speed with the wind: use the distance and time given to calculate the spped:

`\begin{gathered} (240mi)/(2h)=120mi/h \\ \\ x+y=120mi/h \end{gathered}`

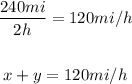
Speed agains the wind: use the distance and time given to calculate the spped:

`\begin{gathered} (240mi)/(3h)=80mi/h \\ \\ x-y=80mi/h \end{gathered}`

System of equations:

`\begin{gathered} x+y=120 \\ x-y=80 \end{gathered}`

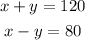
Add both equations:

Use 2x=200 to solve x:

`\begin{gathered} 2x=200 \\ \\ x=(200)/(2) \\ \\ x=100 \end{gathered}`

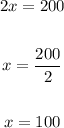
Use x=100 to solve y:

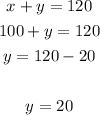
`\begin{gathered} x+y=120 \\ 100+y=120 \\ y=120-20 \\ \\ y=20 \end{gathered}`Then, the rate (speed) of the wind (y) is 20 mi/h