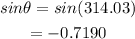SOLUTION
The given function is
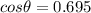
Given that tan θ <0
Notice that the given cosine is positive
Hence the angle is in the first and fourth quadrant
Since it is given that tan θ <0, this implies that tan is negative
Since tan is negative in second and fourth quadrant then the fourth quadrant will be used to defined the value of sine
From the given function
The value of θ is
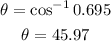
Hence the value of the angle in the fourth quadrant is:
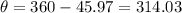
Hence the value of sin θ is