Question

Write each of the following as a function of theta.
1.) sin(pi/4 - theta) 2.) tan(theta+30°)

Answer 1

Explanation:

Let x represent theta.

`\sin( (\pi)/(4) - x )`

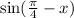
Using the angle addition trig formula,

`\sin(x - y) = \sin(x) \cos(y) - \cos(x) \sin(y)`

`\sin( (\pi)/(4) ) \cos(x) - \cos( (\pi)/(4) ) \sin(x)`

`( ( √(2) )/(2)) \cos(x) - (( √(2) )/(2) )\sin(x)`

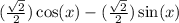
Multiply one side at a time

Replace theta with x , the answer is

`( √(2) \cos(x) )/(2) - ( \sin(x) √(2) )/(2)`

2. Convert 30 degrees into radian

`(30)/(1) * (\pi)/(180) = (\pi)/(6)`

Using tangent formula,

`\tan(x + y) = ( \tan(x) + \tan(y) )/(1 - \tan(x) \tan(y) )`

`( \tan(x) + \tan( (\pi)/(6) ) )/(1 - \tan(x) \tan( (\pi)/(6) ) )`

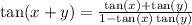
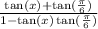
Tan if pi/6 is sqr root of 3/3

`( \tan(x) + ( ( √(3) )/(3) ) )/(1 - \tan(x) (( √(3) )/(3) ) )`

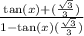
Since my phone about to die if you later simplify that,

you'll get

`\frac{(3 \tan(x) + √(3) )(3 + √(3) \tan(x) }{3(3 - \tan {}^(2) (x) }`

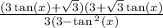
Replace theta with X.