The mean of a data sample can be found by adding all the terms in the data sample and dividing the result by the number of terms. In the first case we have the following data sample:
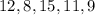
The mean of this sample is:
![\operatorname{mean}=(12+8+15+11+9)/(5)=(55)/(5)=11]()
The mean absolute deviation is the sum of the differences between each data value and the mean, divided by the number of data values, the formula is:

Therefore, we must calculate the positive difference between each value and the mean, add them up, and divide the result by the number of data points in the sample. In the case of the first sample we get:
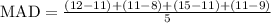
Solving the operation:

If done this way, all the results for each data set must be correct.