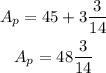Question

Find Area of the polygon for a = 8 %ft b = 5 1/7 ft 10 O 45 sq ft 45/14 sq ft O 41 11/14 sq ft 0 48 3/14 sq ft

Answer 1

To find the area of the polygon we can divide the figure into smaller figures like a rectangle and a triangle.

after we can make the mixed numbers as improper fractions to make them easier to work with

`\begin{gathered} 8(3)/(4)=(8\cdot4+3)/(4)=(35)/(4) \\ 5(1)/(7)=(5\cdot7+1)/(4)=(36)/(7) \end{gathered}`

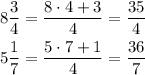
Find the area of the rectangle at the base using the formula

`A=l\cdot w`

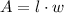
where l is b and w is a

`\begin{gathered} A=(36)/(7)\cdot(35)/(4) \\ A=(1260)/(28) \\ A=45 \end{gathered}`

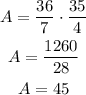
Continue by finding the area of the triangle by the formula

`A=b\cdot(h)/(2)`

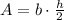
in which b is tha base b and h is the height that is represented by the difference between 10 and a.

`\begin{gathered} A=((36)/(7))\cdot(10-(35)/(4))\cdot(1)/(2) \\ A=((36)/(7))\cdot((5)/(4))\cdot(1)/(2) \\ A=(45)/(14) \\ A=3(3)/(14) \end{gathered}`

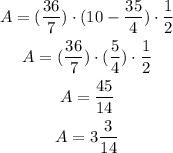
Add both areas together

`\begin{gathered} A_p=45+3(3)/(14) \\ A_p=48(3)/(14) \end{gathered}`