ANSWER

Value of the car after 12 year: $4971.72
Step-by-step explanation
The exponential regression equation is

Using the values of the table we can find both a and b. Note that a is the value of y when x = 0, so a = 13700.
For b replace a, and x and y with the next values of the table:
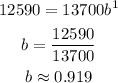
The equation is

To find the value of the car after 12 years, replace x = 12:
