Step 1
Given:
center (0,0)
the equation given should have been:
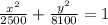
We need to identify the larger denominator. If it is under x, the ellipse is horizontal. If it is under y, the ellipse is vertical. 8100 is the larger denominator and is under y, therefore, the ellipse is vertical
Step 2
The general equation of an ellipse is given as;
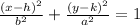
h and k are the center values which are both 0.
a = length of the semi-major axis
b = length of the semi-minor axis
The given equation is;
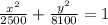
which is equivalent to;

![\begin{gathered} a^2=90^2 \\ \sqrt[]{a^2}=\sqrt[]{90^2} \\ a=90\text{ yard},\text{ the semi-major ax}is \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yldwqr2wlpj75d0im20z3im0gmbjodc684.png)
The length of the major axis will thus be; 90x2=180 yards
Answer; 180 yards