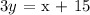Question

2) Write an equation of a line that is parallel to the line whose equation is 3y = x + 6 and that passes through the point (-3,4). Y-Y=m(x-x) y = mx + b ino

Answer 1

Step 1:

In this question, we are given the following:

Write an equation of a line that is parallel to the line whose equation is

`\text{3 y = x + 6}`

and that passes through the point (-3,4)

Step 2:

From the question, we can see that the given equation is given as:

`\begin{gathered} 3\text{ y = x + 6} \\ \text{Divide both sides by 3, we have that:} \\ y\text{ = }(1)/(3)x\text{ + 2} \end{gathered}`

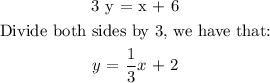
Comparing this, with the equation of a line, we have that:

`\begin{gathered} y\text{ = mx + c} \\ \text{Then, the gradient of line, m = }(1)/(3) \end{gathered}`

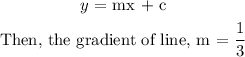
Step 3:

Now, using the equation of a line:

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where (x }_1,y_1)\text{ = ( -3 , 4 )} \\ m\text{ = }(1)/(3) \end{gathered}`
`\begin{gathered} y\text{ - }4\text{ = }(1)/(3)(\text{ x -- 3)} \\ y\text{ - 4 =}(1)/(3)(\text{ x+ 3)} \end{gathered}`

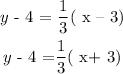
Multiply through by 3, we have that:

`\begin{gathered} \text{3 ( y - 4 ) = ( x + 3)} \\ 3y\text{ - 12 = x + 3} \\ \text{Hence, we have that:} \\ 3y\text{ = x + 3 +1 2} \\ 3\text{ y = x + 15} \end{gathered}`

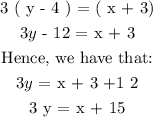
CONCLUSION:

The equation of the line that is parallel to the given line is:

`3y\text{ = x + 15}`