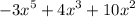Question

Choose the polynomial that is written in standard form.

−3x5 + 4x3 + 10x2
−8x + 4x4 + 3x3
x4 + 4x3 + 10x4
x6 + 4x3 + 10x7

Answer 1

`{ - 3x}^(5) + {4x}^(3) + {10x}^(2)`

Explanation:

For a polynomial to be in standard form, it must satify the conditions below:

1) It must not contain like terms

2) The exponents (powers) must be written in descending order

That is, the polynomial must be of the form

`f(x) = {ax}^(n) + {bx}^(n - 1) + {cx}^(n - 2) + . \: . \: . \: . \: . \: mx + n`

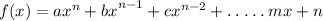
Where a, b, c, m, n, are coefficients/constants

The only option that satifies the above conditions, and follows the pattern f(x) shown is:

`{ - 3x}^(5) + {4x}^(3) + {10x}^(2)`

Answer 2

• A. −3x⁵ + 4x³ + 10x²

Explanation:

• The standard form means that the terms are ordered from biggest exponent to lowest exponent.

Verify the answer options

A. −3x⁵ + 4x³ + 10x²

• 5, 3, 2 - correct order

B. −8x + 4x⁴ + 3x³

• 1, 4, 3 - incorrect order

C. x⁴ + 4x³ + 10x⁴

• 4, 3, 4 - incorrect order

D. x⁶ + 4x³ + 10x⁷

• 6, 3, 7 - incorrect order