When the ball hits the ground, the height of the ball to the ground is h(t) = 0.
Therefore, we can now substitute h(t), and solve the function using quadratic formula.
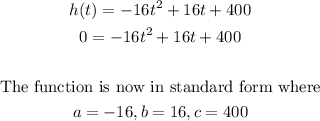
Using the quadratic formula, substitute the following values a,b, and c.
![\begin{gathered} t=( -b \pm√(b^2 - 4ac))/( 2a ) \\ t=( -16 \pm√(16^2 - 4(-16)(400)))/( 2(-16) ) \\ t=\frac{-16\pm\sqrt[]{256-(-25600)}}{-32} \\ t=( -16 \pm√(25856))/( -32 ) \\ t=( -16 \pm16√(101)\, )/( -32 ) \\ \\ t=(-16+16√(101))/(-32) \\ t=-4.52494 \\ \\ t=\frac{-16-16\sqrt[]{101}\, }{-32} \\ t=5.52494 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j9fgsb8s66526d10ndbyn7w1b7cxcr0a7q.png)
We have two solutions, t = -4.52494, and t = 5.52494. However, we will disregard the negative time value.
Therefore, the ball will hit the ground after 5.52494 seconds.