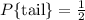Question

A fair coin is tossed 3 times in succession. The set of equally likely outcomes is (HHH, HHT, HTH, THH, HTT, THT, TTH, TTT). Find the probability of getting a tailon the second toss

Answer 1

A fiar coin is tossed 3 times in succession.

The results for each experiment is displayed as follows;

`\begin{gathered} \text{HHH} \\ \text{HHT} \\ \text{HTH} \\ \text{THH} \\ \text{HTT} \\ \text{THT} \\ \text{TTH} \\ \text{TTT} \end{gathered}`

On each toss from the above results, the probability of getting a tail would include all results that has a tail come up. That would be;

`P\lbrack\text{Event\rbrack}=\frac{\text{Number of required outcomes}}{Number\text{ of all possible outcomes}}`
`P\lbrack\text{tail\rbrack}=(4)/(8)`

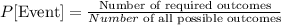
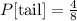
Note that to get a tail on the "second toss" would mean to get a result with a tail as the second out of three. We have 7 outcomes with tails. However 4 of these has a tail as a second outcome, hence we have the required outcome as 4 out of a total of 8.

ANSWER:

Probability of getting a tail on the second toss is

`P\mleft\lbrace\text{tail}\mright\rbrace=(1)/(2)`