Question

5) A ball is dropped from a height of 400 feet. Each time it hits the ground, it rebounds 75% of the distance it has fallen. How far will the ball travel before coming to rest?

Answer 1

Initial height: 400 m

Each time it hits the ground, it rebounds 75% the distance it has fallen. Let us say this distance is d, then the new height is:

`\begin{gathered} h=75\text{\% of }d=(75)/(100)\cdot d \\ \Rightarrow h=(3)/(4)d \end{gathered}`

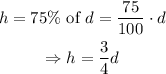
If the initial height is 400 m, then the subsequent heights are given by the recurrence equation:

`\begin{gathered} h_0=400 \\ h_n=((3)/(4))^n\cdot h_0 \\ \Rightarrow h_n=400\cdot((3)/(4))^n \end{gathered}`

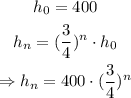
And the total distance traveled D is:

`\begin{gathered} D=h_0+2\cdot\sum ^(\infty)_(n\mathop=1)\lbrack((3)/(4))^n\cdot h_0\rbrack \\ \Rightarrow D=400+800\cdot\sum ^(\infty)_{n\mathop{=}1}((3)/(4))^n \end{gathered}`

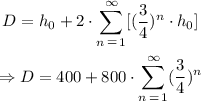
Now, let us analyze the sum term:

`\sum ^(\infty)_{n\mathop{=}1}((3)/(4))^n=(3)/(4)+((3)/(4)_{})^2+((3)/(4))^3+\cdots_{}`

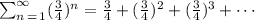
From the infinite geometric sequence:

`\begin{gathered} \sum ^(\infty)_(n\mathop=0)r^n=(1)/(1-r) \\ \Rightarrow\sum ^(\infty)_{n\mathop{=}1}r^n=(1)/(1-r)-1 \end{gathered}`

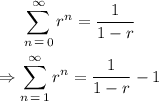
Where r < 1. From our problem, r = 3/4 < 1, then:

`\begin{gathered} \sum ^(\infty)_{n\mathop{=}1}((3)/(4))^n=(1)/(1-(3)/(4))-1=(1)/((1)/(4))-1=4-1 \\ \Rightarrow\sum ^(\infty)_{n\mathop{=}1}((3)/(4))^n=3 \end{gathered}`

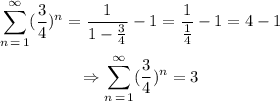
Finally, using this result:

`D=400+800\cdot3=400+2400=2800`