Question

27) Suppose object A has double the specific heat and triple the mass of object B. If the same amount of heat is applied to both objects, how will the temperature change of A be related to the temperature change of B? Enter your answer to three significant figures.

Answer 1

The absorbed or released by a system is given by the following formula:

`Q=m\cdot Cp\cdot\Delta T`

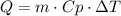
Where Q is the heat absorbed or released, m is the mass of the system, Cp is the specific heat and ΔT is the change in the temperature.

Let mA and mB be the mass of objects A and B, let CpA and CpB be the specific heats of objects A and B and let ΔTA and ΔTB be the specific heats of objects A and B. We will have that:

`\begin{gathered} mA=3mB \\ CpA=2CpB \end{gathered}`

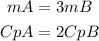
If the same amount of heat is applied to both object, we will have that:

`\begin{gathered} QA=QB \\ mA\cdot CpA\cdot\Delta TA=mB\cdot CpB\cdot\Delta TB \end{gathered}`

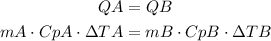
Replace mA and CpA for their equivalences in terms of mB and CpB:

`\begin{gathered} 3mB\cdot2CpB\cdot\Delta TA=mB\cdot CpB\cdot\Delta TB \\ \Delta TA=(mB)/(3mB)\cdot(CpB)/(2CpB)\cdot\Delta TB \\ \Delta TA=(1)/(3)\cdot(1)/(2)\Delta TB \\ \Delta TA=(1)/(6)\Delta TB \end{gathered}`

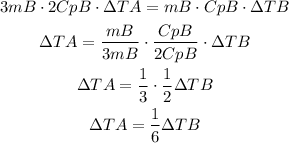
It means that the change in temperature of A is 1/6 of the change of temperature of B.

`\Delta TA=(1)/(6)\Delta TB`