Question

Solve the following inequalities and give the solutions in both set and interval notations.

-x/8 + 8/3 ≥ 3

Answer 1

Given:

The inequality is

`-(x)/(8)+(8)/(3)\geq 3`

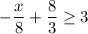
To find:

The solution for the given inequality in both set and interval notations.

Solution:

We have,

`-(x)/(8)+(8)/(3)\geq 3`

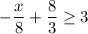
It can be written as

`-(x)/(8)\geq 3-(8)/(3)`

`-(x)/(8)\geq (9-8)/(3)`

`-(x)/(8)\geq (1)/(3)`

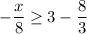
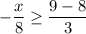
Multiply both sides by -8 and change the inequality sign.

`x\leq -(8)/(3)`

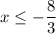
It means all the values of
`x` which are less than or equal to
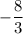`-(8)/(3)` are included in the solution set.

Set notation is
`\x`.

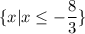Interval notation is
`\left(-\infty,-(8)/(3)\right ]`.