Question

A ballistic pendulum consists of a 1.25-kg block of wood that is hanging from the ceiling in such a way that when a bullet enters it, the block’s change in height can be recorded as it swings. A bullet having a mass of 6.25-grams and unknown velocity strikes the block and becomes imbedded in it. The impulse imparted to the block causes it to swing in such a way that its height increases by 7.15 cm.1. What was the change in potential energy of the block/bullet combo after the collision?2. What was the speed of the block/bullet combo immediately after the collision (and before it beganto swing)?3. What was the speed of the bullet before entering the block of wood?

Answer 1

1.

The potential energy is defined as:

`U=mgh`

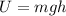
The change in potential energy is:

`\Delta U=U_f-U_i`

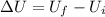
the initial height of the block/bullet is zero, then we have that:

`\begin{gathered} \Delta U=(1.25+0.00625)(9.8)(0.0715)-0 \\ \Delta U=0.8802 \end{gathered}`

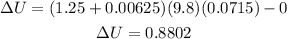
Therefore, the change in potential energy is 0.8802 J

2.

We know that the energy is conserved, this means that the kinetic energy inmediately after collision has to be equal to the potential energy at the 7.15 cm heigh, then we have:

`\begin{gathered} (1)/(2)mv^2=0.8802 \\ (1)/(2)(1.25625)v^2=0.8802 \\ v=\sqrt[]{(2\cdot0.8802)/(1.25625)} \\ v=1.184 \end{gathered}`

Therefore, the velocity at this moment is 1.184 m/s

3.

From conservation of momentum we know that:

`m_bv_b=mv`

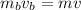
then:

`\begin{gathered} (0.00625)v_b=(1.25625)(1.184) \\ v_b=((1.25625)(1.184))/(0.00625) \\ v_b=237.98 \end{gathered}`

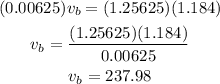
Therefore the speed of the bullet is 237.98 m/s