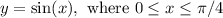Question

Find the equation of the curve that passes through the point (x, y) = (0, 0) and has an arc length on the interval x is between 0 and pi over 4 inclusive given by the integral the integral from 0 to pi over 4 of the square root of the quantity 1 plus the cosine squared x, dx . (5 points)

Answer 1

`\displaystyle y=\sin(x),\text{ where } 0\leq x\leq\pi/4`

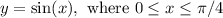
Explanation:

The curve passes through the point (x, y) = (0, 0) and has an arc length on the interval [0, π/4] given by the integral:

`\displaystyle \int_(0)^(\pi/4)√(1+\cos^2(x))\, dx`

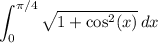
And we want to find the equation of the curve.

Recall that arc length is given by:

`\displaystyle L=\int_a^b\sqrt{1+\Big((dy)/(dx)\Big)^2}\, dx`

Rewrite our original integral:

`\displaystyle \int_(0)^(\pi/4)√(1+(\cos(x))^2)\, dx`

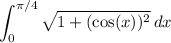
So:

`\displaystyle (dy)/(dx)=\cos(x)`

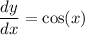
It follows that:

`\displaystyle y=\sin(x)+C`

Using the initial condition:

`0=\sin(0)+C\Rightarrow 0=0+C\Rightarrow C=0`

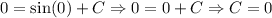
The equation for our curve is:

`\displaystyle y=\sin(x),\text{ where } 0\leq x\leq\pi/4`