The expression we have is:
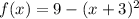
We need to compare this expression with the Vertex form of the quadratic equation:
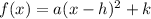
Where the vertex is at (h,k).
We rewrite our expression as follows:
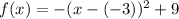
And we can see that h=-3, and k=9. Thus, the vertex of this quadratic function is at:
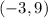
Also, since we have a negative sign along side the x, that means that the parabola opens down.
And the correct result is:
Option C