Question

A woman tries to throw a rock over a wall, releasing the rock at a height of 1.55m abovethe ground. If she throws the rock at 6 m/s, will it reach the top of the wall 3.75m aboveher?

Answer 1

`H_(\max )-H_{\text{wall}}=-0.3635m\Rightarrow Negative`

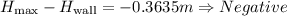
Step-by-step explanation: We need to find if the rock can reach the height of the wall, provided the initial velocity of 6m/s and it is thrown from the height of 1.55m above the ground., the equations used to solve this problem are as follows:

`\begin{gathered} v(t)=v_o-gt\Rightarrow(1) \\ y(t)=y_o+v_ot-(1)/(2)gt^2\Rightarrow(2) \end{gathered}`

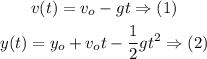
Plugging in the known values in the equation (1) and (2) we get the following results:

`\begin{gathered} v(t)=6ms^(-1)-(9.8ms^(-2))t\Rightarrow(3) \\ y(t)=1.55m+(6ms^(-1))t-(1)/(2)(9.8ms^(-2))t^2\Rightarrow(4) \\ \end{gathered}`

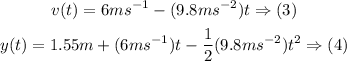
Setting equation (3) equal to zero gives the time to reach the maximum height as follows:

`\begin{gathered} v(t)=6ms^(-1)-(9.8ms^(-2))t=0 \\ t=((6ms^(-1)))/((9.8ms^(-2)))=0.61s \\ t=0.61s \end{gathered}`

Substituting the time t calculated above in equation (4) gives the maximum height, the steps for the calculation are shown as follows:

`\begin{gathered} y(0.62)=1.55m+(6ms^(-1))(0.62s)-(1)/(2)(9.8ms^(-2))(0.62s)^2 \\ y(0.62)=1.55m+3.72m-1.88356m=3.3865m \\ y(0.62)=3.3865m \\ H_(\max )=3.3865m \\ H_(\max )-H_{\text{wall}}=3.3865m-3.75m=-0.3635m\Rightarrow Negative \\ \\ \end{gathered}`

Therefore, the ball can not reach the height of the wall!