Question

Consider the diagram of a combination circuit below on the left. In the middle, the resistors in the two parallel branches have been replaced by a single resistor (R4) with an equivalent resistance to the overall branch resistors. On the right, all three resistors have been replaced by a single resistor (R5) with an equivalent resistance as all three original resistors. Suppose that you know that:R1 = 24.8ΩR2 = 24.8ΩR3 = 12.7Ω What must R4 and R5 be in order for the two circuits to have the same equivalent resistance? R4 = ------- Ω R5 = ----- Ω

Answer 1

Given:

• R1 = 24.8Ω

,

• R2 = 24.8Ω

,

• R3 = 12.7Ω

From the diagram, let's find R4 and R5.

We can see that the 3 resistors R1, R2, and R3 are connected in parallel.

Where:

R1 + R2 = R4

To solve for R4, we have:

`(1)/(R_4)=(1)/(R_1)+(1)/(R_2)`

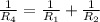
Thus, we have:

Now, to solve for R5 since R3 and R4 are now in series, we have:

`\begin{gathered} R_5=R_3+R_4 \\ \\ R_5=12.7+12.4 \\ \\ R_5=25.1Ω \end{gathered}`

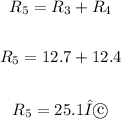
Therefore, we have:

R4 = 12.4 Ω

R5 = 25.1 Ω

ANSWER:

• R4 = 12.4 ,Ω

,

• R5 = 25.1 ,Ω