Question

4. Tickets for a carnival cost $6 for adults and $4 for children. The school has abudget of $120 for a field trip to the carnival. An equation representing thebudget for the trip is 120 = 6x + 4y. Here is a graph of this equation:

Answer 1

Given:

The equation is 6x + 4y = 120.

Step-by-step explanation:

The points that lies on the line satifies the equation. So point (0,30) lies on the number which 0 adults and 30 children could go to school. So "if no adult chaperons were needed, 30 students could go to school is true.

For ten students and 15 adults point is (15,10). The point (15,10) does not lie on number line and not satifies the equation so second statement is false.

The cost of tickets for 4 adults is,

`4\cdot6=24`

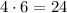
and cost of tickets for six students is,

`6\cdot4=24`

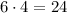
Both costs are equal, means for six fewer students 4 additional adults can go to the zoo. Thus third statement is correct.

The cost of tickets for two children is,

`4\cdot2=8`

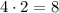
The cost of tickets for 3 adults is,

`6\cdot3=18`

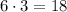
Since cost of tickets for 3 adults is more than cost of tickets for two children which means two children can not go to the zoo for 3 fewer adults in the trip. Thus fourth statement is wrong.

For 16 adults and 6 students point is (16,6). The point (16,6) lies on the number line, which point (16,6) satifies the equation. So fifth statement is correct.