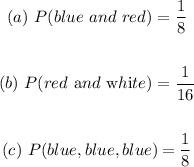Question

Manuel has a bag of marbles with 2 blue marbles, 1 white marbles, and 1 red marbles.Find the following probabilities of Manuel drawing the given marbles from the bag if the first marble(s) is(are) returned to the bag after they are drawn.a) a blue, then a red b) a red, then white c) a blue, then a blue, then a blue

Answer 1

Explanation

We are given the following:

`\begin{gathered} Bag=\begin{cases}{2\text{ }blue\text{ }marbles} \\ {1\text{ }white\text{ }marbles} \\ {1\text{ }red\text{ }marbles}\end{cases} \\ Total\text{ }marbles=2+1+1=4 \end{gathered}`

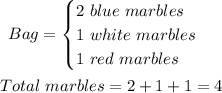
We are required to determine the following probabilities:

`\begin{gathered} (a)\text{ }a\text{ }blue,\text{ }then\text{ }a\text{ }red \\ (b)\text{ }a\text{ }red,\text{ }then\text{ }white \\ (c)\text{ }a\text{ }blue,\text{ }then\text{ }a\text{ }blue,\text{ }then\text{ }a\text{ }blue \end{gathered}`

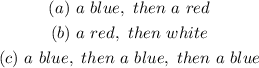
We know that probability is calculated as:

`Prob.=\frac{Number\text{ }of\text{ }required\text{ }outcome}{Number\text{ }of\text{ }possible\text{ }or\text{ }total\text{ }outcome}=(n(E))/(n(S))`

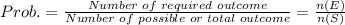
For Question A:

We can determine the probability of a blue, then a red as:

`\begin{gathered} P(blue\text{ }and\text{ }red)=P(Blue)* P(Red) \\ =(2)/(4)*(1)/(4)=(2)/(16)=(1)/(8) \\ \therefore P(blue\text{ }and\text{ }red)=(1)/(8) \end{gathered}`

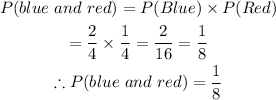
For Question B:

We can determine the probability of a red, then white as:

For Question C:

We can determine the probability of a blue, then blue, then blue as:

`\begin{gathered} P(blue,blue,blue)=P(blue)* P(blue)* P(blue) \\ =(2)/(4)*(2)/(4)*(2)/(4)=(1)/(2)*(1)/(2)*(1)/(2)=(1)/(8) \\ \therefore P(blue,blue,blue)=(1)/(8) \end{gathered}`

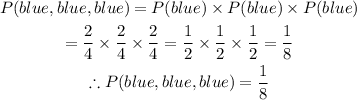
Hence, the answers are:

`\begin{gathered} (a)\text{ }P(blue\text{ }and\text{ }red)=(1)/(8) \\ \\ (b)\text{ }P(red\text{ a}nd\text{ w}h\mathrm{i}te)=(1)/(16) \\ \\ (c)\text{ }P(blue,blue,blue)=(1)/(8) \end{gathered}`