Question

The height of a triangle is 3 feet less than the base. The area of the triangle is 230 square feet. Find the length of the baseand the height of the triangle,

Answer 1

Let b be the base of the traingle

Let h be the height of the triangle

The height of a triangle is 3 feet less than the base:

`h=b-3`

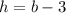
The area of the triangle is 230 square feet.

The area of a triangle is:

`A=(1)/(2)(b\cdot h)`

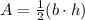
For the given triangle:

`\begin{gathered} A=(1)/(2)(b\cdot(b-3)) \\ \\ 230=(1)/(2)(b\cdot(b-3)) \end{gathered}`

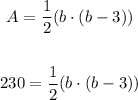
Solve b in the equation above:

`\begin{gathered} 230=(b^2-3b)/(2) \\ \\ 2\cdot230=b^2-3b \\ \\ 460=b^2-3b \\ \\ b^2-3b-460=0 \end{gathered}`

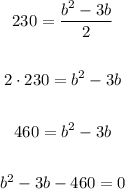
Use the quadratic formula:

`\begin{gathered} ax^2+bx+c=0 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ \end{gathered}`
`\begin{gathered} b=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(1)(-460)}}{2(1)} \\ \\ b=\frac{3\pm\sqrt[]{9+1840}}{2} \\ \\ b=\frac{3\pm\sqrt[]{1849}}{2} \\ \\ b=(3\pm43)/(2) \\ \\ b_1=(3+43)/(2)=(46)/(2)=23 \\ \\ b_2=(3-43)/(2)=-(40)/(2)=-20 \end{gathered}`

As the length of the base cannot be a negative quantity you use the solution 1.

The base of the triangle is 23ft

Use the value of b to find the heigth:

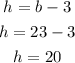
`\begin{gathered} h=b-3 \\ h=23-3 \\ h=20 \end{gathered}`Then, the given triangle has the next dimensions:base: 23ftheight: 20ft