Solution
Discriminant
- The formula for the discriminant of a quadratic equation is:
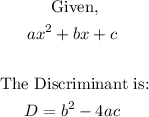
- Applying the formula, we have:

- Discriminant is 33
How many solutions
- If the discriminant is > 0, then, the Quadratic equation has 2 solution.
- If the discriminant is = 0, then, the Quadratic equation has 1 solution
- If the discriminant is < 0, then, the Quadratic equation has no real solutions.
- The discriminant is 33 > 0, thus, the Quadratic equation has 2 solutions
Type of zero
- Since there are 2 solutions, then, it has real solutions
Final Answer
OPTION B